Given a \(n \times m\) grid with numbered cells and forbidden cells, the objective of the Rogo puzzle is to find a loop of fixed length through the grid such that the sum of the numbers in the cells on the loop is maximized.
Problem Statement
Rogo is a puzzle game that was developed in 2009 by Nicola Petty and Shane Dye, who are faculty members at the University of Canterbury in Christchurch, New Zealand.
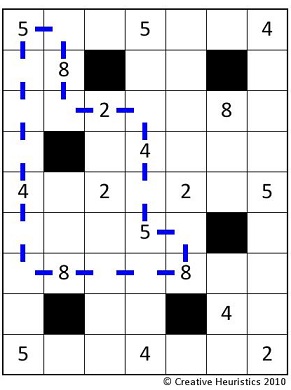
Given a rectilinear grid with numbered squares and forbidden squares, the objective of Rogo is to find a loop of fixed length (pre-specified) with the maximum score. The score is calculated by summing the numbers in the squares on the loop. The rules of the game are (1) the loop can start on any square, (2) the loop must end at the starting square, (3) the loop may contain only horizontal and vertical steps (diagonal steps are forbidden), (4) the loop may visit a square at most once, and (5) the loop may not include any forbidden squares. A loop with a length of 20 steps and a score of 44 is shown in the grid below.
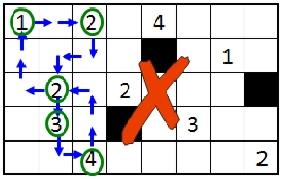
An example of an illegal move is shown in the grid below; the move is illegal because the square with the “2” in the second column has already been visited on the loop.
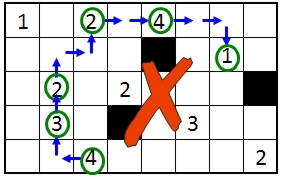
An example of an illegal loop is shown below; the loop does not return to its starting point.
Solve the Puzzle
For the best results, we recommend using Firefox for this interactive case study.
Select any square to begin. As you select squares, the first box shows the number of steps remaining and the second box shows the current score. To submit the problem to NEOS to find the maximum score, click on the “Solve with NEOS” button. Have fun!
| Select a puzzle |
| # Steps Left: | |
| Score: | |
| Solution Edges: |
Mathematical Formulation
Given an \(n \times m\) grid with numbered cells and forbidden cells, the objective of Rogo is to find a loop of fixed length through the grid such that the sum of the numbers in the cells of the loop is maximized. The key to the formulation is writing constraints to enforce the loop requirements:
- the loop must start and end at the same cell,
- each non-forbidden cell may be visited at most once,
- the loop must be exactly the number of specified steps.
Rogo is an example of a puzzle based on a well-known and extensively studied operations research problem called the Traveling Salesman Problem (TSP). Given a list of cities and their pairwise distances, the objective of the TSP is to find the shortest possible tour that visits each city exactly once. Rogo is a special case of the TSP. Because Rogo has a limit on the number of steps and not every cell (city) can be visited, it is a subset-selection TSP. Also, because some of the cells in Rogo have a reward value, it is similar to the prize-collecting TSP.
The general formulation of the asymmetric TSP is provided below, where \(V\) is the set of cities. The binary variable \(x_{ij}\) takes the value of 1 if the salesman travels between city \(i\) and city \(j\), and the distance \(d_{ij}\) is the distance to travel from \(i\) to \(j\). The first constraint set specifies that there must be an edge that leaves city \(i\). The second constraint set specifies that there must be an edge that enters city \(j\). These two sets of constraints are not sufficient to enforce the loop conditions, however, since they allow for “subtours”, which are disjoint loops. The third constraint set is the subtour elimination constraint set, which specifies that every subset \(S\) of cities may contain at most \(|S|-1\) edges.
TSP Formulation
Minimize \(\sum_{i \in V}\sum_{j \in V} d_{ij}*x_{ij}\)
subject to
\(\sum_{j \in V} x_{ij} = 1, \forall i \in V\)
\(\sum_{i \in V} x_{ij} = 1, \forall j \in V\)
\(\sum_{i \in S}\sum_{j \in S} x_{ij} \le |S| – 1, \forall S \subseteq V, 2 \le |S| \le |V| – 1\)
Note that since the formulation requires a constraint for each subset \(S\), there can be a very large (exponential) number of subtour elimination constraints. An alternate formulation includes the Miller-Tucker-Zemlin (MTZ) constraints. The formulation with the MTZ constraints is a weaker formulation but it includes a smaller (polynomial) number of constraints. The MTZ formulation is often sufficient for small instances. Let \(u_i\) be the position of city \(i\) in the tour. Then, the MTZ constraints are:
\(u_1 =1\)
\(2 \leq u_i \leq |V|, \forall i \neq 1\)
\(u_i – u_j + 1 \leq (|V|-1)(1 – x_{ij}), \forall 1 \leq i \neq j \leq n\)
Rogo Formulation
The TSP formulation with the MTZ constraints is a starting point for the formulation of Rogo. The following modifications are required:
- There are forbidden cells in the grid, so not all arcs are allowed. A set of feasible arcs is defined.
- The loop does not need to visit every cell, so knowing the starting point is required. A binary variable, \(\delta_i\), is defined to indicate whether or not cell \(i\) is the starting point of the loop.
Sets
\(V\) = set of cells
\(A\) = set of feasible arcs
Parameters
\(n\) = number of steps
\(p_i\) = value of cell \(i\), \(\forall i \in V\)
Variables
\(x_{ij} = \left\{ \begin{array}{ll}
1 & \mbox{if arc \((i,j)\) is in the loop, \(\forall (i,j) \in A\)} \\
0 & \mbox{otherwise}
\end{array} \right. \)
\(y_i = \left\{ \begin{array}{ll}
1 & \mbox{if cell \(i\) is in the loop, \(\forall i \in V\)} \\
0 & \mbox{otherwise}
\end{array} \right. \)
\(\delta_i = \left\{ \begin{array}{ll}
1 & \mbox{if cell \(i\) is the starting point, \(\forall i \in V\)} \\
0 & \mbox{otherwise}
\end{array} \right. \)
\(u_i\) = position of cell \(i\) in the loop, \(\forall i \in V\)
Maximize \(\sum_{i \in V} p_i y_i\)
Subject to:
1. The loop must have \(n\) steps.
\(\sum_{i \in V} y_i = n\)
2. If a cell is entered, it must be exited.
\(\sum_{j:(i,j) \in A} x_{ij} = y_i, \forall i \in V\)
\(\sum_{i:(i,j) \in A} x_{ij} = y_j, \forall j \in V\)
3. If cell \(i\) is the starting point, its relative position in the loop should be exactly one.
\(u_i – \delta_i \geq 0\)
\(u_i + (n – 1)*\delta_i \leq n\)
4. The loop can have only one starting point.
\(\sum_{i \in V} \delta_i = 1\)
5. The MTZ constraints are modified to accommodate that not every cell is visited.
\(u_i – u_j + n*(x_{ij} – \delta_j) \leq n-1, 1 \leq i \neq j \leq n\)
To solve this mixed integer linear programming problem, we can use one of the NEOS Server solvers in the Mixed Integer Linear Programming (MILP) category. Each MILP solver has one or more input formats that it accepts.
GAMS Model
As an example, we provide a GAMS model for “Introductory Rogo #3” puzzle from the Rogo website.
set V /1*40/;
scalars nrow /5/, ncol /8/;
scalar steps /12/;
alias(V,i,j);
set arc(i,j);
parameter p(V) /1 2, 2 0, 3 3, 4 0, 5 1, 6 0, 7 0, 8 2,
9 0, 10 3, 11 0, 12 0, 13 0, 14 0, 15 4, 16 0,
17 4, 18 0, 19 1, 20 0, 21 0, 22 4, 23 0, 24 1,
25 0, 26 0, 27 -100, 28 2, 29 2, 30 -100, 31 0, 32 0,
33 0, 34 0, 35 2, 36 0, 37 0, 38 2, 39 0, 40 0/;
arc(i,j) = yes\$(abs(ord(i)-ord(j))=ncol or (ord(j)-ord(i))\$(mod(ord(i),ncol) ne 0 and
mod(ord(j),ncol) ne 1)=1 or (ord(i)-ord(j))\$(mod(ord(j),ncol) ne 0 and mod(ord(i),ncol) ne 1)=1);
binary variable
y(V)
x(i,j)
delta(v);
positive variable
u(V);
variable
obj;
equations
connections(i)
connections2(j)
loop_size
mtz(i,j)
assign1(V)
assign2(V)
objective
assign3;
objective.. sum(v,p(v)*y(v)) =e= obj;
loop_size.. sum(V,y(V)) =e= steps;
connections(i).. sum(j\$arc(i,j),x(i,j)) =e= y(i);
connections2(j).. sum(i\$arc(i,j),x(i,j)) =e= y(j);
assign1(V).. u(V)-delta(V) =g= 0;
assign2(V).. u(V) +(steps-1)*delta(V) =l= steps;
assign3.. sum(V,delta(V)) =e= 1;
mtz(i,j)$(ord(i) ne ord(j)).. u(i)-u(j) + steps*(x(i,j)-delta(j)) =l= steps-1;
model project /all/;
solve project using mip max obj;
References
- Balas, E., The prize collecting traveling salesman problem. Carngie Mellon University, Pittsburg, Pennsylvania. http://onlinelibrary.wiley.com/doi/10.1002/net.3230190602/pdf
- Linderoth, J. Tools and Environment in Optimization (ISyE/CS 635). University of Wisconsin – Madison. May 2011.
- Operations research, Sudoko, Rogo, and Puzzles. Retrieved from Michael Trick’s Operations Research Blog, http://mat.tepper.cmu.edu/blog/?p=1302
- Petty, N. & Dye, S. (2010). Determining degree of difficulty in Rogo, a TSP-based paper puzzle. Proceedings of the 45th Annual Conference of the ORSNZ, November 2010.
- Rogo – the New Puzzle Game (2011), by Creative Heuristics Ltd. Retrieved from http://www.rogopuzzle.co.nz/
Original contribution by Jackie Lamb and Nanjing Jian, May 2011.
